14 VERTICES YIELD 16383 COMBINATIONS.
SOME COMBINATIONS WORK AND SOME DON’T.
AND, BELIEVE IT OR NOT, SOME COMBINATIONS YIELD ONLY TILINGS WHICH ARE NEITHER PERIODIC NOR APERIODIC. (See Section 6, below.)
by Paul Hofmann
1. THE STATE OF THE ART
From Wolfram Alpha, slightly condensed:
“A demi-regular tessellation, also called a polymorph tessellation, is a type of tessellation whose definition is somewhat problematic. Some authors define it as an orderly composition of the 3 regular tessellations and the 8 semiregular tessellations (which is not precise enough to draw any conclusions from), while others define it as a tessellation having more than one transivity class of vertices (which leads to an infinite number of possible tilings).
“The number of demi-regular tessellations is commonly given as 14 (Critchlow, Ghyka, Williams, Steinhaus). However, not all sources apparently give the same 14. Caution is therefore needed in attempting to determine what is meant by ‘demi-regular tessellation.’
“A more precise term of demi-regular tessellation is 2-uniform tessellation (Grunbaum and Shepard). There are 20 such tessellations (Krotenheerdt).”
IN OTHER WORDS, IT’S A MESS !
Let’s see if we can straighten it out…
2. THE BIG LIST
Leaving out the octagon (which will tile only with the square), there are 14 ways that the 4 useable regular polygons (triangle, square, hexagon, and dodecagon) will fit around a vertex. In dual tilings, these 14 vertices become 14 distinct dual polygons. For every tiling of regular polygons there is a tiling of dual polygons and vice versa. They are each other’s skeletons.
Let’s say that we label each of these 14 dual polygons (or, if you prefer, each of these 14 vertices of regular polygons—it amounts to the same thing) with a letter of the alphabet, A through N. How many ways can these 14 letters be combined? The answer is: 16383 combinations in 14 Groups consisting of combinations of from 1 to 14 letters respectively. This is the Big List.
What would happen if we tested every one of these 16383 combinations, in order to find out which combinations will tile the plane, without gaps or overlaps, in at least one way?
AS FAR AS I KNOW, THIS QUESTION HAS NEVER BEFORE BEEN ASKED, LET ALONE ANSWERED.
The Big List System is made possible by two simple shifts. First, the shift of focus from the 14 vertices of regular polygons to the 14 dual polygons generated by those vertices. Second, the shift in notation from descriptive strings to sets of single-letter symbols. The Big List could not be written out and explored without these two changes.
The 14 Groups of the 16383 candidate-combinations break down like this: 14, 91, 364, 1001, 2002, 3003, 3492, 3003, 2002, 1001, 364, 91, 14, and 1.
Successful combinations in the 14 Groups are as follows: Groups 1, 2, 3, and 4 yield 10, 16, 44, and 82 successes respectively. Groups 13 and 14 yield 12 successes and 1 success respectively. Groups 5, 6, 7, 8, 9, 10, 11, and 12 each yield many successes, but I do not expect to check anywhere near all 14958 candidates in these 8 middle groups in my lifetime.
All possible tilings (an infinite number) of the 4 regular polygons and of the 14 dual polygons have a place in the Big List system. This is the global rather than the myopic view of tilings of regular polygons. It seems to me that the emphasis on regular, semi-regular, and “demi-regular” (whatever that means) tilings in the literature, along with the grotesque terminology, tangled prose, and awkward systems of notation, has discouraged the exploration of a potential cornucopia of beautiful and interesting patterns.
3. WORKING WITH THE BIG LIST
The Big List may be written out by hand on graph paper. Two columns of 50 combinations each will just about fill a page. If you start a new page for each of the 14 Groups, you will need 173 pages in all. Putting the 14 letters across the top of each of the two columns and then placing each letter of each combination in its proper stack will make it easier to read the combinations.
Of course, if you know how to write code, you could probably generate the list that way. I don’t, so I wrote out the whole list myself, 114,688 letters in all. Twice, to get it right. (See sample pages below.)
Note that usually a capital letter without brackets, such as A, B, or C, refers to a particular dual polygon, while a capital letter (or group of capital letters) with brackets, such as [A], [AB], or [ABC], refers to a candidate-combination, successful or otherwise. (On a graph-paper list the brackets are not necessary.)
Once you have the Big List you will be ready to try out all 16383 candidate-combinations to see which ones will tile the plane. This will take you a while.
Or you might want to just try a few combinations at random from each of the 14 Groups.
Here are some sample pages of the Big List.
4. TESTING THE COMBINATIONS
The Vertex Chart (way up above) shows the 14 possible arrangements of the 4 regular polygons around a vertex and also shows the 14 dual polygons that these 14 arrangements generate.
There are 3 ways that you can test a combination:
By drawing. Sketching the regular polygons is easy because all the sides are the same length. You just have to get used to the angles. Then draw in the dual polygons in a different color line.
By manipulating cardboard or paper tiles. Each polygon shape, regular or dual, should get its own color.
There are of course various drawing programs available. That’s fine if you already know what tiling you want to draw. But to move tiles around, a dedicated drag-and-dock program would be very handy.
There are 2 shortcuts you can use to eliminate candidates just by looking at the letters. These shortcuts seem to eliminate about half of the candidates. But the survivors will still have to be tested. The shortcuts are to eliminate candidates, not to confirm them.
SHORTCUT #1
The dual polygon pair AM will only tile the plane in a combination having a total of 4 or more distinct dual polygons. And so on, as below:
Pairs which will only work in combinations of 4 or more different tiles: AM, AN, BG, BN, CE, CF, DN, EJ, EL, FJ, FM, IL, and LM.
Pairs requiring combinations of 5 or more different tiles: AH, BH, CH, CK, CL, CM, EK, EM, EN, GL, HI, HJ, IK, IN, and MN.
Pairs requiring combinations of 6 or more different tiles: CN, FK, GK, GN, and HM.
Pairs requiring combinations of 7 or more different tiles: FN, HK, and HL
Pair requiring combinations of 8 or more different tiles: HN
SHORTCUT #2
H will not tile the plane without F (except solo), and so on, as below:
H requires F.
C requires A or I.
N requires K or L.
G requires E, F, or I.
M requires I, J, or K.
D requires A, B, E, F, or K.
L requires A, B, J, K, or N.
J requires A, B, I, K, L, or M.
E requires A, B, D, F, G, I, or K.
F requires A, B, D, E, G, H, I, or K.
B requires A, D, E, F, I, J, K, or L.
A requires B, C, D, E, F, I, J, K, or L.
K requires A, B, D, E, F, I, J, L, M, or N.
I requires A, B, C, E, F, G, J, K, L, or M.
5. ORGANIZING THE SUCCESSFUL COMBINATIONS
Successful combinations are identified by numbers. For example, [A] is No. 1, [DE] is No. 17, [FGH] is No. 63, and so on. Each successful combination gets only one identification number whether it is singular or infinitely variable. Note that a successful combination in the latter part of the list cannot be assigned a number until all combinations have been tested up to that point.
The 16383 candidate-combinations can be organized not only by Group but by Class and by Family.
There are 15 possible sets of the 4 regular polygons, but only 10 of these sets yield tilings. These are the 10 Classes. The 14 Groups and the 10 Classes can be combined in a Big Grid of 140 slots, with the 14 Groups listed crosswise and the 10 Classes listed lengthwise. Only 43 of the slots will contain successful tilings and those comprise the 43 Families of tilings of regular polygons and their duals. Every tiling in a particular Family will have the same set of regular polygons and the same set of dual polygons.
LIST OF CLASSES
Class 1 [3-4-6-12] 15,214 candidates > ? successes
Class 2 [3-4-6] 977 candidates > 353 successes
Class 3 [3-4-12] 110 candidates > 32 successes
Class 4 [3-6] 29 candidates > 19 successes
Class 5 [3-4] 13 candidates > 10 successes
Class 6 [4-6-12] 4 candidates > 1 success
Class 7 [3-12] 2 candidates > 1 success
Class 8 [3] 1 candidate > 1 success
Class 9 [4] 1 candidate > 1 success
Class 10 [6] 1 candidate > 1 success
Class 11-x [3-6-12] 30 candidates > 0 successes
Class 12-x [4-6] 1 candidate > 0 successes
Class 13-x [4-12] 0 candidates > 0 successes
Class 14-x [6-12] 0 candidates > 0 successes
Class 15-x [12] 0 candidates > 0 successes
TOTAL: 16383 candidates > ? total successes
(For LIST OF FAMILIES, scroll way down, almost to the bottom.)
6. SPECIAL TILINGS
At least 31 successful combinations are singular. That is, they will tile in only one way. Most likely all other successful combinations will tile in an infinite number of ways. I have never found a combination that will tile in only a finite number of ways above 1.
At least 28 combinations will tile only periodically.
At least 14 combinations will not tile the plane either periodically or aperiodically, yet will tile the plane without gaps or overlaps. How can that be? One would think that if a combination is able to tile at all, it must tile either periodically or aperiodically or both. But in order for a tiling to qualify as aperiodic (according to the literature), it must not have “arbitrarily large” areas of periodicity. And since these 14 combinations always generate tilings with “arbitrarily large” areas of periodicity, they cannot be said to tile aperiodically. Yet they will not tile periodically either. So how do they tile? The answer is that they will tile only radially. (For example see illustration [ABL] below.) As far as I know, this distinction does not appear anywhere in the literature on tilings of regular polygons and their duals. No notches, markings, or matching rules necessary, though tile-flipping must be allowed. However, in 3 of the 14 cases, [ABL], [ABCJL], and [ABEGJ], there are no chiral tiles, so tile-flipping is neither necessary nor possible in those 3 cases.
At least 3 combinations will tile only chirally. That is, only in both right- and left-handed versions.
The known (by me, at this time) special tilings are as follows:
Singular: [A], [B], [C], [D], [E], [G], [H], [J], [M], [N], [AJ], [DF], [DK], [IJ], [ABK], [ABL], [BDI], [BDK], [BEI], [BFI], [BIJ], [BKL], [ABIM], [AFIJ], [AFIM], [BCFI], [BDFI], [BDKL], [BEFI], [BEIL], and [BFIM].
Periodic only: [A], [B], [C], [D], [E], [G], [H], [J], [M], [N], [AJ], [DF], [DK], [IJ], [BDI], [BDK], [BEI], [BFI], [BIJ], [BKL], [AFIJ], [AFIM], [BCFI], [BDFI], [BDKL], [BEFI], [BEIL], and [BFIM].
Radial only: [ABI], [ABK], [ABL], [ABCI], [ABGI], [ABIM], [ABKL], [ABCJL], [ABEGJ], [ABEIL], [ABEIM], [ABFHI], [ABIJM], and [ABKLN]. There may be more in Group 6 or higher.
Chiral only: [E], [ABL], and [BKL].
Singular, periodic only, and chiral only: [E] and [BKL].
Singular, radial only, and chiral only; the rarest of the rare: [ABL].
7. A FEW EXAMPLES OF NOTABLE TILINGS
[ABL]. Singular, radial only, chiral only. The only tiling of dual polygons that falls into all 3 of these categories. (Below)
[CIJ]. Most successful combinations will tile in an infinite number of ways. Variations are usually achieved by such simple operations as rotating, shifting, repeating, or alternating. [CIJ] is unusual in that it has variations which are structurally distinct. (Below)
[ABCJ]. An example of a combination that will tile both periodically and radially. (Below)
[ABDE]. Another example of a combination that will tile both periodically and radially. (Below)
[BKL]. Singular, periodic only, chiral only. One of only two such tilings. (Below)
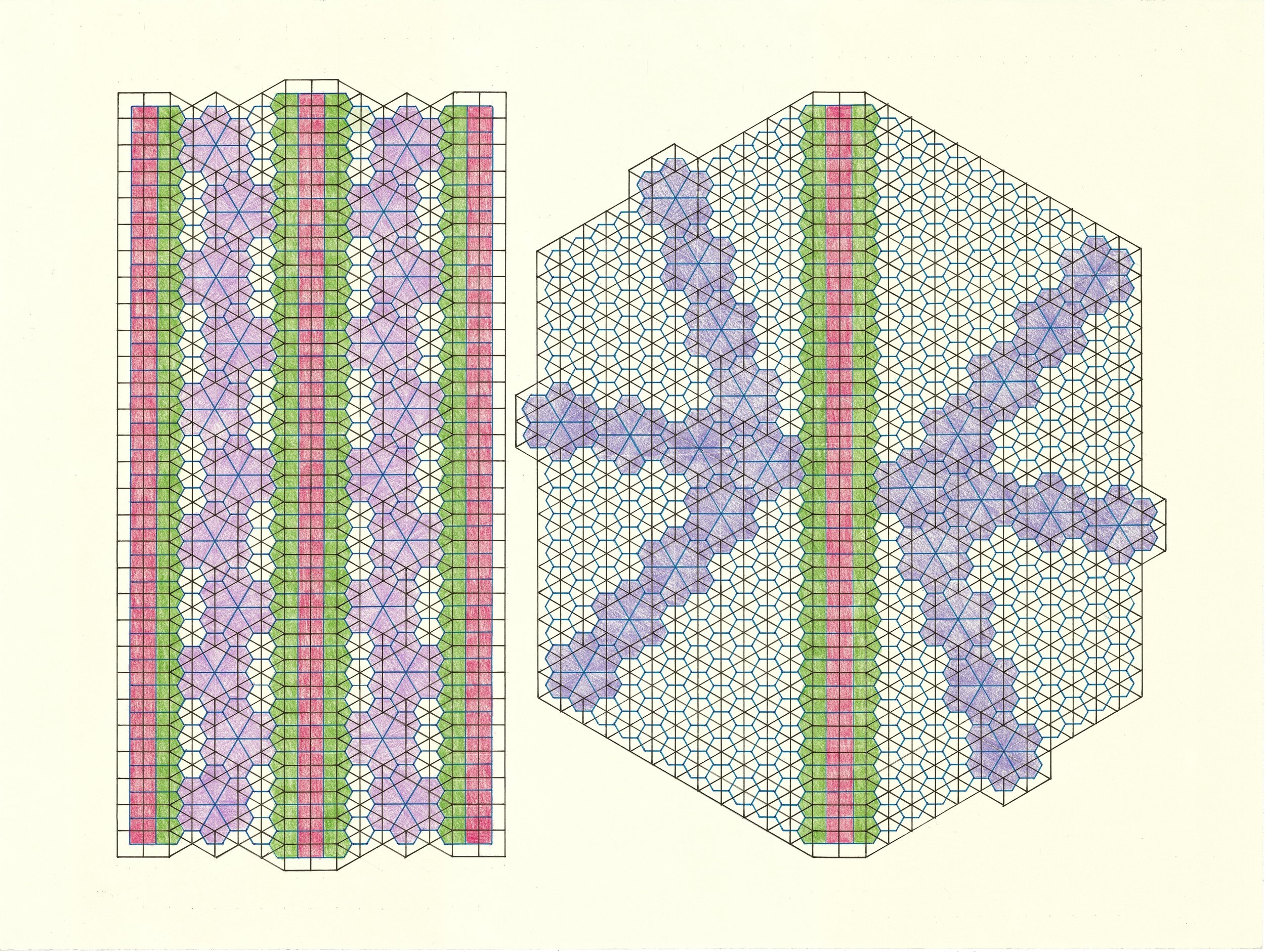
[ABCDL] Twelve infinitely long expanding spokes, one infinitely long uniform-width spoke, and an infinitely expanding whirlpool-like spiral. (Below)
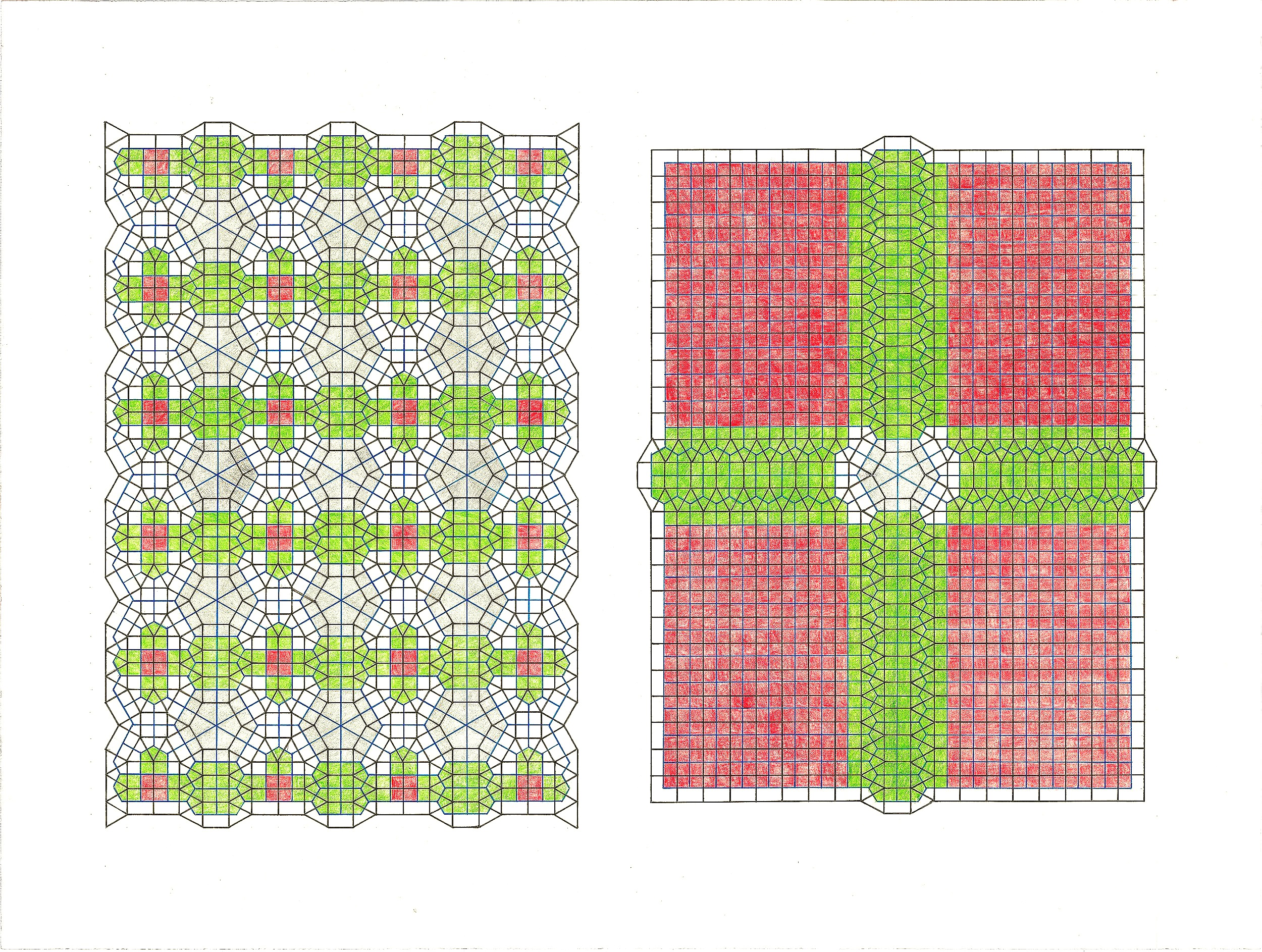
[BDJKM]. There are 12 ways that sets of infinitely long parallel lines can be configured in dual tilings, considering both the number of different sets and their angles relative to each other (but ignoring the distance between parallel lines). [BDJKM] can be rearranged to show 10 of those ways. This particular version shows 4 sets at 30, 30, 30, and 90 degrees. (Below)
[ABCDEFGHIJKLMN]. This sole member of Group 14 will tile in an infinite number of ways. Here’s one of them. (Below)
And, just to show that it can be done, here are some random successful combinations, one from each of the 14 Groups: [E], [AB], [JKN], [DEFH], [ABDKN], [BGIJKLN], [DEFGHIJ], [ABEFHIKN], [ABCEFGHIJ], [ABCDEFGHIJ], [ABCDEFGHIJN], [ABCDEFGHIJMN], [ACDEFGHIJKLMN], and [ABCDEFGHIJKLMN].
The possibilities are endless. Better to explore the big picture and see what’s there than to decide in advance what to look for. Go, Grove City.
8. MISCELLANEOUS NOTES
~ 1 ~ Leaving the regular octagon in the System would give us 16384 additional candidate-combinations, only one of which would work. And we already know about that one.
~ 2 ~ Counting the 3 chiral polygons (I, K, and M) as 6 distinct polygons would increase the Big List by 114,688 candidates without adding a single success, since those 3 dual polygons always occur in right- and left-handed pairs in tilings of regular polygons.
~ 3 ~ One standard way of labeling a particular combination is with a string of numbers, superscripts, and punctuation marks. For instance, using this method, [BDJKM] would be notated as [3(2).4.3.4;3.4.6.4;3(2).4.12;4.6.12]. (The two numerals in parentheses represent superscripts—no thanks to Squarespace for this!). Imagine this kind of notation being used for combinations in Groups 12, 13, or 14. Worse yet, imagine the entire Big List of 16383 combinations notated in this way!
~ 4 ~ We have seen that there are 14 ways that the 4 regular polygons will fit around a vertex and that these 14 types of vertex yield 16383 testable combinations. So how many ways will the 14 dual polygons fit around a vertex? The answer is 648. And how many testable combinations will those 648 vertexes yield? The math is beyond me, but the number must be truly astronomical.
~ 5 ~ Each of the 14 dual polygons may be found embedded in a dodecagram (12-pointed star) of configuration 1-6-11-4-9-2-7-12-5-10-3-8-1. A circle may be drawn in the center of the dodecagram in such a way that it is tangent to each side of each of the 14 dual polygons. The diameter of the circle is the same as the lengths of each side of each of the 4 regular polygons. (I was not the first to discover this connection.)
~ 6 ~ Historically, there seems to have been some puzzlement as to why no other regular polygons are compatible in tilings of regular polygons. The reason they are not compatible is that all the angles of all the regular polygons (and all the dual polygons) in this system must be evenly divisible by 30. This requirement also explains why the regular octagon is a dead-end and doesn’t belong in the system despite the fact that it will tile with the square.
~ 7 ~ Convex equilateral polygons having 5, 7, 8, 9, and 10 sides, all angles divisible by 30, do exist, but, because they are not equiangular, they are not regular polygons. They will, however, tile with the regular polygons. In fact, they are built out of regular polygons. But will they tile with each other? And what about the duals? This seems to be an unexplored area in the world of tilings.
~ 8 ~ For combinations that will tile in only one way, I use the word “singular” rather than the word “unique” because the latter word has been rendered meaningless from misuse.
~ 9 ~ If you draw any one of the infinite number of tilings of regular polygons, and then overlay it with its dual tiling, using the same color line for both, you will see that you have made a new tiling. And you will see, every time, that this new tiling is made of one or more of the following 4 tiles: square, small kite, big kite, and long kite. And so, with just those 4 tiles, you can build any tessellation of regular polygons with its dual tessellation already in place.
~ 10 ~ If you draw a tiling of regular hexagons and overlay it with its dual tessellation of regular triangles, (again, using the same color line for both the hexagons and the triangles), you will see a new tiling built exclusively with big kites. And this new tiling can then be used as a template for a tessellation of Einstein tiles. Or… you can draw a tiling of regular triangles and overlay it with its dual tessellation of regular hexagons and, again, you will see that this new tiling is made of big kites, but on a smaller scale, and still useful as a template for Einstein tiles, likewise on a smaller scale.
~ 11 ~ There are no mathematical or geometrical breakthroughs here. I have simply devised a system of organization that includes all the possibilities—something that could have and should have been done a long time ago. After all, it has been well over 2000 years since Archimedes gave us the regular and semi-regular tilings.
~ 12 ~ Questions, comments, additions, suggestions, or corrections? Email me at: paulhofmann@earthlink.net. (Please note: one F and two NNs.)
~ 13 ~ See also: phsculpture.com.
9. LIST OF FAMILIES OF TILINGS OF REGULAR POLYGONS:
Family 1: Group 1 - Class 2 2 candidates > 1 success
Family 2: Group 1 - Class 4 3 candidates > 2 successes
Family 3: Group 1 - Class 5 2 candidates > 2 successes
Family 4: Group 1 - Class 6 1 candidate > 1 success
Family 5: Group 1 - Class 7 1 candidate > 1 success
Family 6: Group 1 - Class 8 1 candidate > 1 success
Family 7: Group 1 - Class 9 1 candidate > 1 success
Family 8: Group 1 - Class 10 1 candidate > 1 success
Family 9: Group 2 - Class 1 25 candidates > 1 success
Family 10: Group 2 - Class 2 28 candidates > 4 successes
Family 11: Group 2 - Class 3 14 candidates > 2 successes
Family 12: Group 2 - Class 4 10 candidates > 5 successes
Family 13: Group 2 - Class 5 6 candidates > 4 successes
Family 14: Group 3 - Class 1 202 candidates > 8 successes
Family 15: Group 3 - Class 2 106 candidates > 19 successes
Family 16: Group 3 - Class 3 31 candidates > 7 successes
Family 17: Group 3 - Class 4 5 candidates > 7 successes
Family 18: Group 3 - Class 5 4 candidates > 3 successes
Family 19: Group 4 - Class 1 747 candidates > 23 successes
Family 20: Group 4 - Class 2 204 candidates > 47 successes
Family 21: Group 4 - Class 3 34 candidates > 7 successes
Family 22: Group 4 - Class 4 1 candidate > 1 success
Family 23: Group 4 - Class 5 1 candidate > 1 success
Family 24: Group 5 - Class 1 1723 candidates > ? successes
Family 25: Group 5 - Class 2 251 candidates > 76 successes
Family 26: Group 5 - Class 3 21 candidates > 9 successes
Family 27: Group 5 - Class 4 1 candidate > 1 success
Family 28: Group 6 - Class 1 2786 candidates > ? successes
Family 29: Group 6 - Class 2 210 candidates > 95 successes
Family 30: Group 6 - Class 3 7 candidates > 6 successes
Family 31: Group 7 - Class 1 3311 candidates > ? successes
Family 32: Group 7 - Class 2 120 candidates > 68 successes
Family 33: Group 7 - Class 3 1 candidate > 1 success
Family 34: Group 8 - Class 1 2958 candidates > ? successes
Family 35: Group 8 - Class 2 45 candidates > 33 successes
Family 36: Group 9 - Class 1 1992 candidates > ? successes
Family 37: Group 9 - Class 2 45 candidates > 9 successes
Family 38: Group 10 - Class 1 1000 candidates > ? successes
Family 39: Group 10 - Class 2 1 candidate > 1 success
Family 40: Group 11 - Class 1 364 candidates > ? successes
Family 41: Group 12 - Class 1 91 candidates > ? successes
Family 42: Group 13 - Class 1 14 candidates > 12 successes
Family 43: Group 14 - Class 1 1 candidate > 1 success
TOTAL: 16,383 candidates > ? successes
10: ADDENDUM: MAGIC SQUARES AND THE BIG PICTURE:
And by the way, the BIG-PICTURE APPROACH also yields interesting results when applied to 4x4 magic squares (1-16, sum 34).
How many ways can 16 numbers be arranged in a 4x4 square? Just multiply 16 x 15 x 14 x 13 x 12 x 11 x 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 and you get 20,922,789,888,000.
By the year 1675, Bernard Frenicle de Bessy had determined that only 880 of those 21 trillion arrangements of 16 numbers are magic squares. (I doubt that he checked them all.)
But in each and every one of those 880 magic squares (and in each of the trillions of un-magic ones too) there are 86 ways that 4 of the 16 numbers add up to 34.
So how many ways can 4 numbers be arranged in a 4x4 square? By convention, only a few arrangements are recognized in magic squares, generally rows or blocks.
But in fact there are 1820 possible arrangements of 4 cells in every magic square. These 1820 arrangements can be divided into 3 categories: primary, secondary, and tertiary, as follows:
There are 100 primary arrangements, 10 lines, 20 squares, 26 rectangles, and 44 parallelograms.
There are 204 secondary arrangements, all of them having bilateral symmetry, whether horizontal, vertical, or diagonal: 68 tees, 64 wyes, 56 trapezoids, and 20 crisscrosses.
There are 1516 tertiary arrangements: miscellaneous asymmetrical quadrilaterals and trilaterals (the latter having their extra cell either contained in the interior or embedded in a side).
In conclusion: Multiplying 1820 possible arrangements of 4 cells times 86 possible sets of 4 numbers (1-16) yields 156,520 possible arrangements of 4 numbers (1-16) adding up to 34.
And that is the big picture!